
Zadanie Proste (pro)
Pomóż nam usprawnić bazę zadań!
Proste
Limit pamięci: 32 MB
Na płaszczyźnie dany jest zbiór 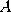 złożony z
złożony z  punktów. Odległością prostej
punktów. Odległością prostej 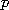 od zbioru
od zbioru 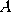 nazywamy
największą spośród odległości punktów ze zbioru
nazywamy
największą spośród odległości punktów ze zbioru 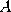 do prostej
do prostej 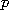 . Spośród wszystkich prostych przechodzących
przez pewien ustalony punkt
. Spośród wszystkich prostych przechodzących
przez pewien ustalony punkt 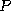 należy wybrać taką, której odległość do zbioru
należy wybrać taką, której odległość do zbioru 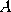 jest możliwie najmniejsza.
Jako odpowiedź należy wypisać na standardowe wyjście odległość tej prostej od zbioru
jest możliwie najmniejsza.
Jako odpowiedź należy wypisać na standardowe wyjście odległość tej prostej od zbioru 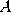 .
.
Zadanie
Napisz program, który:
- wczyta ze standardowego wejścia opis zbioru
 i położenie punktu
i położenie punktu 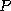 ,
,
- wyliczy minimalną odległość od zbioru
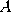 ,
,
- wypisze ją na standardowe wyjście.
Wejście
W pierwszym wierszu znajduje się jedna liczba całkowite  (
(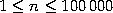 ).
W drugim wierszu znajdują się dwie liczby całkowite - współrzędne punktu
).
W drugim wierszu znajdują się dwie liczby całkowite - współrzędne punktu  .
W każdej z kolejnych
.
W każdej z kolejnych  linii znajdują się dwie liczby całkowite - współrzędne kolejnych punktów ze zbioru
linii znajdują się dwie liczby całkowite - współrzędne kolejnych punktów ze zbioru 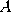 . Wiadomo, że wartości bezwzględne wszystkich współrzędnych nie przekraczają
. Wiadomo, że wartości bezwzględne wszystkich współrzędnych nie przekraczają 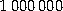 .
.
Wyjście
Wyjśćie powinno zawierać dokładnie jedną liczbę rzeczywistą oznaczającą szukaną odległość z dokładnie trzema miejscami po
przecinku i zaokrągloną w dół. Testy dobrane są tak, że popełnienie błędu mniejszego niż 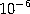 gwarantuje
uzyskanie poprawnego wyniku po zaokrągleniu.
gwarantuje
uzyskanie poprawnego wyniku po zaokrągleniu.
Przykład
Dla danych wejściowych:
8 3 3 3 1 9 1 7 4 10 4 4 5 1 6 5 9 8 8
poprawną odpowiedzią jest:
4.472
Autor zadania: Jakub Pawlewicz.
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English